MECÂNICA GERAL
Pelo método de integrais, usando área diferencial. determine a centroide na figura abaixo.
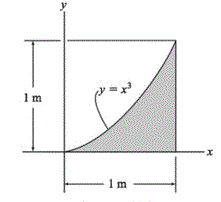
X = 0,9 m e Y= 0,63 m
X = 0,35 m e Y= 0,6 m
X = 0,8 m e Y= 0,286 m
X = 1,1 m e Y= 0,45 m
X = 0,65 m e Y= 0,26 m
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.
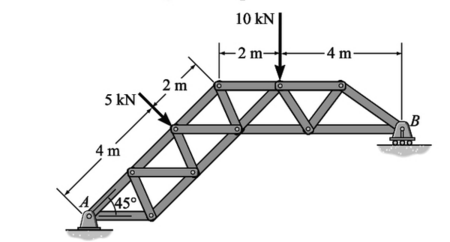
Bx=By= 7,25 kN
Bx= 7,25 kN
By= 7,25 kN
By= 8,05 kN
Bx= 8,05 kN
Determine os componentes horizontal e vertical em A. Despreze a espessura da viga.
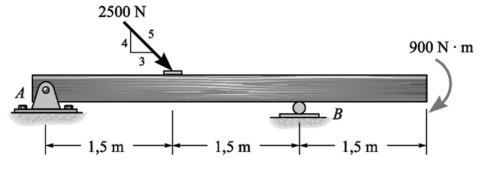
Ax= 1300 N
Ay= 600 N
Ax= 1300 N
Ay= 800 N
Ax= 500 N
Ay= 600 N
Ax= 900 N
Ay= 800 N
Ax= 1500 N
Ay= 700 N
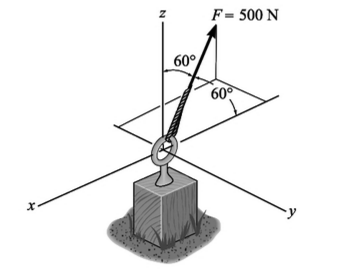
O parafuso tipo gancho mostrado na figura está sujeito a duas forças F1e F2. Determine o módulo e a direção da força resultante.
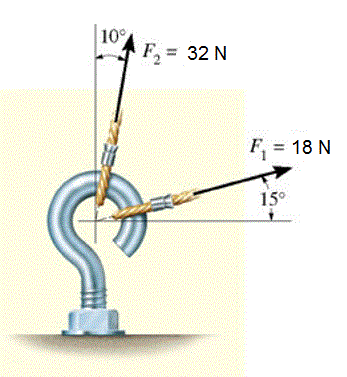
Fr = 52,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 31,34° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 57,61° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 37,38° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
A tração no cabo AC da figura ao abaixo é de 370 N. O valor da componente vertical da força exercida em C é aproximadamente
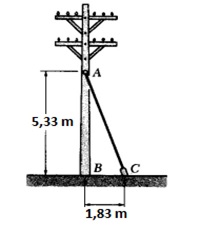
268,50 N
295,82 N
378,75 N
349,95 N
189,45 N
Qual função em relação a distância x, representa o esforço cortante e o momento fletor na viga abaixo.
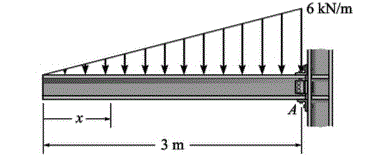
V= 2x-1
M= - x³/3
V= x+4
M= - x²+2x-1
V= - x²
M= - x³/3
V= x-5
M= x²-x
V= - 2x³
M= - x²/5
Determine o esforço cortante em C e o momento fletor em D da viga. Assuma que B seja um rolete e que C está localizado logo à direita da carga de 40 kN.
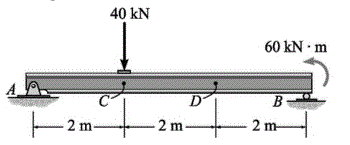
VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = 4,8 kN
MD = - 75,8 kN.m
A região do pé esta sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.
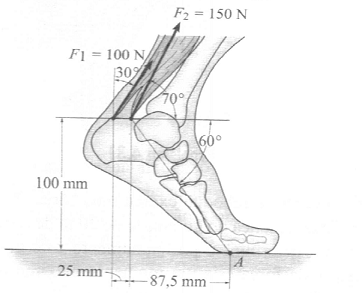
13,21 N.m, 19,13 N.m
10,25 N.m, 13,43 N.m
32,25 N.m, 4,12 N.m
21,15 N.m, 16,28 N.m
14,74 N.m, 17,46 N.m
Considere o arco a seguir,
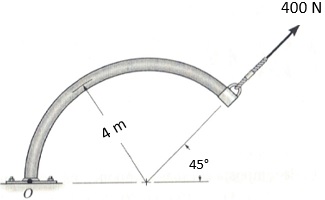
O momento da força em relação ao ponto O é aproximadamente

X = 0,9 m e Y= 0,63 m
X = 0,35 m e Y= 0,6 m
X = 0,8 m e Y= 0,286 m
X = 1,1 m e Y= 0,45 m
X = 0,65 m e Y= 0,26 m
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.

Bx=By= 7,25 kN
Bx= 7,25 kN
By= 7,25 kN
By= 8,05 kN
Bx= 8,05 kN
Determine os componentes horizontal e vertical em A. Despreze a espessura da viga.

Ax= 1300 N
Ay= 600 N
Ax= 1300 N
Ay= 800 N
Ax= 500 N
Ay= 600 N
Ax= 900 N
Ay= 800 N
Ax= 1500 N
Ay= 700 N
O parafuso tipo gancho mostrado na figura está sujeito a duas forças F1e F2. Determine o módulo e a direção da força resultante.

Fr = 52,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 31,34° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 57,61° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 37,38° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
A tração no cabo AC da figura ao abaixo é de 370 N. O valor da componente vertical da força exercida em C é aproximadamente

268,50 N
295,82 N
378,75 N
349,95 N
189,45 N
Qual função em relação a distância x, representa o esforço cortante e o momento fletor na viga abaixo.

V= 2x-1
M= - x³/3
V= x+4
M= - x²+2x-1
V= - x²
M= - x³/3
V= x-5
M= x²-x
V= - 2x³
M= - x²/5
Determine o esforço cortante em C e o momento fletor em D da viga. Assuma que B seja um rolete e que C está localizado logo à direita da carga de 40 kN.

VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = 4,8 kN
MD = - 75,8 kN.m
A região do pé esta sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.

13,21 N.m, 19,13 N.m
10,25 N.m, 13,43 N.m
32,25 N.m, 4,12 N.m
21,15 N.m, 16,28 N.m
14,74 N.m, 17,46 N.m
Considere o arco a seguir,

O momento da força em relação ao ponto O é aproximadamente
Bx=By= 7,25 kN
Bx= 7,25 kN
By= 7,25 kN
By= 8,05 kN
Bx= 8,05 kN
Determine os componentes horizontal e vertical em A. Despreze a espessura da viga.

Ax= 1300 N
Ay= 600 N
Ax= 1300 N
Ay= 800 N
Ax= 500 N
Ay= 600 N
Ax= 900 N
Ay= 800 N
Ax= 1500 N
Ay= 700 N
O parafuso tipo gancho mostrado na figura está sujeito a duas forças F1e F2. Determine o módulo e a direção da força resultante.

Fr = 52,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 31,34° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 57,61° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 37,38° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
A tração no cabo AC da figura ao abaixo é de 370 N. O valor da componente vertical da força exercida em C é aproximadamente

268,50 N
295,82 N
378,75 N
349,95 N
189,45 N
Qual função em relação a distância x, representa o esforço cortante e o momento fletor na viga abaixo.

V= 2x-1
M= - x³/3
V= x+4
M= - x²+2x-1
V= - x²
M= - x³/3
V= x-5
M= x²-x
V= - 2x³
M= - x²/5
Determine o esforço cortante em C e o momento fletor em D da viga. Assuma que B seja um rolete e que C está localizado logo à direita da carga de 40 kN.

VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = 4,8 kN
MD = - 75,8 kN.m
A região do pé esta sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.

13,21 N.m, 19,13 N.m
10,25 N.m, 13,43 N.m
32,25 N.m, 4,12 N.m
21,15 N.m, 16,28 N.m
14,74 N.m, 17,46 N.m
Considere o arco a seguir,

O momento da força em relação ao ponto O é aproximadamente

Ax= 1300 N
Ay= 600 N
Ax= 1300 N
Ay= 800 N
Ax= 500 N
Ay= 600 N
Ax= 900 N
Ay= 800 N
Ax= 1500 N
Ay= 700 N
O parafuso tipo gancho mostrado na figura está sujeito a duas forças F1e F2. Determine o módulo e a direção da força resultante.

Fr = 52,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 31,34° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 57,61° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 37,38° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
A tração no cabo AC da figura ao abaixo é de 370 N. O valor da componente vertical da força exercida em C é aproximadamente

268,50 N
295,82 N
378,75 N
349,95 N
189,45 N
Qual função em relação a distância x, representa o esforço cortante e o momento fletor na viga abaixo.

V= 2x-1
M= - x³/3
V= x+4
M= - x²+2x-1
V= - x²
M= - x³/3
V= x-5
M= x²-x
V= - 2x³
M= - x²/5
Determine o esforço cortante em C e o momento fletor em D da viga. Assuma que B seja um rolete e que C está localizado logo à direita da carga de 40 kN.

VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = 4,8 kN
MD = - 75,8 kN.m
A região do pé esta sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.

13,21 N.m, 19,13 N.m
10,25 N.m, 13,43 N.m
32,25 N.m, 4,12 N.m
21,15 N.m, 16,28 N.m
14,74 N.m, 17,46 N.m
Considere o arco a seguir,

O momento da força em relação ao ponto O é aproximadamente

Fr = 52,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 31,34° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 57,61° em relação à horizontal no sentido anti horário.
Fr = 52,83 N
θ = 37,38° em relação à horizontal no sentido anti horário.
Fr = 42,83 N
θ = 27,38° em relação à horizontal no sentido anti horário.
A tração no cabo AC da figura ao abaixo é de 370 N. O valor da componente vertical da força exercida em C é aproximadamente

268,50 N
295,82 N
378,75 N
349,95 N
189,45 N
Qual função em relação a distância x, representa o esforço cortante e o momento fletor na viga abaixo.

V= 2x-1
M= - x³/3
V= x+4
M= - x²+2x-1
V= - x²
M= - x³/3
V= x-5
M= x²-x
V= - 2x³
M= - x²/5
Determine o esforço cortante em C e o momento fletor em D da viga. Assuma que B seja um rolete e que C está localizado logo à direita da carga de 40 kN.

VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = 4,8 kN
MD = - 75,8 kN.m
A região do pé esta sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.

13,21 N.m, 19,13 N.m
10,25 N.m, 13,43 N.m
32,25 N.m, 4,12 N.m
21,15 N.m, 16,28 N.m
14,74 N.m, 17,46 N.m
Considere o arco a seguir,

O momento da força em relação ao ponto O é aproximadamente

268,50 N
295,82 N
378,75 N
349,95 N
189,45 N
Qual função em relação a distância x, representa o esforço cortante e o momento fletor na viga abaixo.

V= 2x-1
M= - x³/3
V= x+4
M= - x²+2x-1
V= - x²
M= - x³/3
V= x-5
M= x²-x
V= - 2x³
M= - x²/5
Determine o esforço cortante em C e o momento fletor em D da viga. Assuma que B seja um rolete e que C está localizado logo à direita da carga de 40 kN.

VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = 4,8 kN
MD = - 75,8 kN.m
A região do pé esta sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.

13,21 N.m, 19,13 N.m
10,25 N.m, 13,43 N.m
32,25 N.m, 4,12 N.m
21,15 N.m, 16,28 N.m
14,74 N.m, 17,46 N.m
Considere o arco a seguir,

O momento da força em relação ao ponto O é aproximadamente

V= 2x-1
M= - x³/3
V= x+4
M= - x²+2x-1
V= - x²
M= - x³/3
V= x-5
M= x²-x
V= - 2x³
M= - x²/5
Determine o esforço cortante em C e o momento fletor em D da viga. Assuma que B seja um rolete e que C está localizado logo à direita da carga de 40 kN.

VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = 4,8 kN
MD = - 75,8 kN.m
A região do pé esta sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.

13,21 N.m, 19,13 N.m
10,25 N.m, 13,43 N.m
32,25 N.m, 4,12 N.m
21,15 N.m, 16,28 N.m
14,74 N.m, 17,46 N.m
Considere o arco a seguir,

O momento da força em relação ao ponto O é aproximadamente

VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = 4,8 kN
MD = - 75,8 kN.m
A região do pé esta sujeita à contração dos dois músculos plantarflexor. Determine o momento de cada força em relação ao ponto de contato A no chão.

13,21 N.m, 19,13 N.m
10,25 N.m, 13,43 N.m
32,25 N.m, 4,12 N.m
21,15 N.m, 16,28 N.m
14,74 N.m, 17,46 N.m
Considere o arco a seguir,

O momento da força em relação ao ponto O é aproximadamente

13,21 N.m, 19,13 N.m
10,25 N.m, 13,43 N.m
32,25 N.m, 4,12 N.m
21,15 N.m, 16,28 N.m
14,74 N.m, 17,46 N.m
Considere o arco a seguir,

O momento da força em relação ao ponto O é aproximadamente